La moyenne de l’échantillon implique la moyenne de l’échantillon obtenue aléatoirement de l’ensemble de la population. Population La moyenne n’est que la moyenne de l’ensemble du groupe. Jetez un coup d'œil à cet article pour connaître les différences entre la moyenne de l'échantillon et la moyenne de la population.
Tableau de comparaison
| Base de comparaison | Moyenne d'échantillon | Population signifie |
|---|---|---|
| Sens | La moyenne de l'échantillon est la moyenne arithmétique des valeurs d'échantillonnage aléatoires tirées de la population. | La moyenne de la population représente la moyenne réelle de l'ensemble de la population. |
| symbole | x̄ (prononcé comme x bar) | μ (terme grec mu) |
| Calcul | Facile | Difficile |
| Précision | Faible | Haute |
| Déviation standard | Lorsqu'il est calculé en utilisant la moyenne de l'échantillon, il est désigné par (s). | Lorsqu'il est calculé en utilisant la moyenne de la population, il est noté (σ). |
Définition de la moyenne d'échantillon
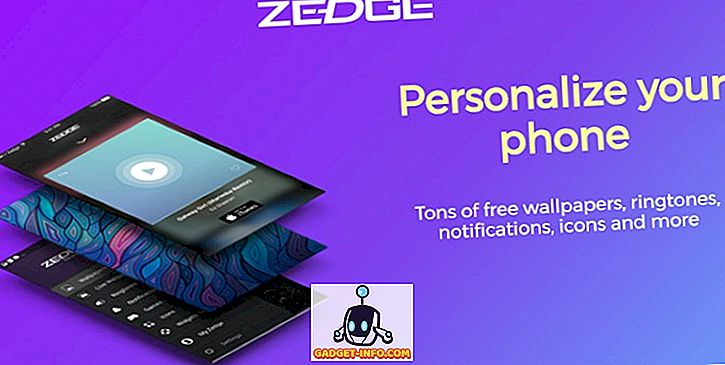
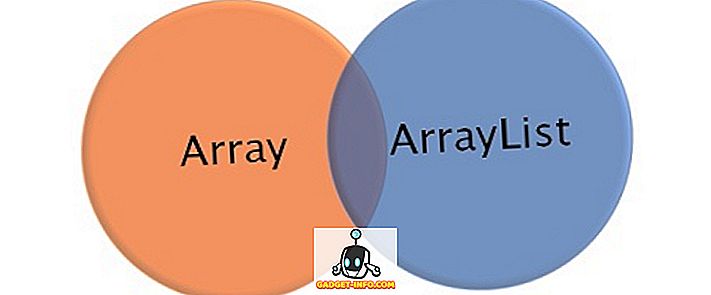
La moyenne de l'échantillon est la moyenne calculée à partir d'un groupe de variables aléatoires, tiré de la population. Il est considéré comme un estimateur efficace et sans biais de la moyenne de la population, ce qui signifie que la statistique la plus attendue pour la statistique de l'échantillon est la statistique de la population, quelle que soit l'erreur d'échantillonnage. La moyenne de l'échantillon est calculée comme suit:

∑ = ajouter
a i = toutes les observations
Définition de la population moyenne
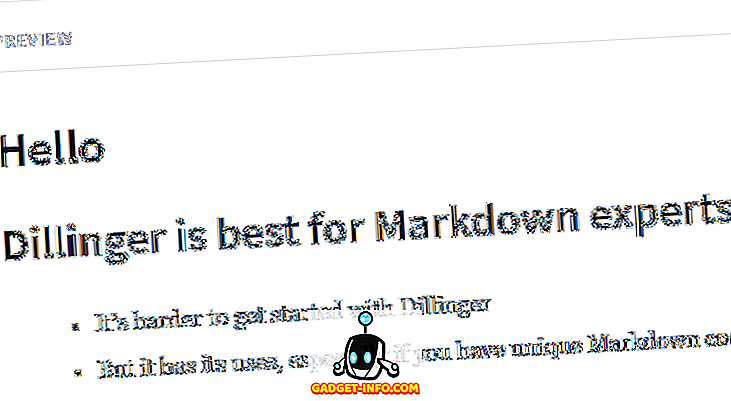
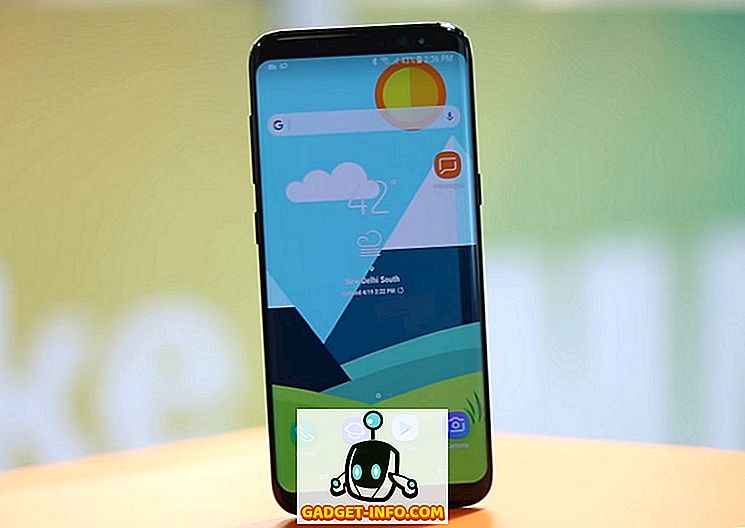
Dans Statistiques, la moyenne de la population est définie comme la moyenne de tous les éléments de la population. C'est un moyen de caractéristique de groupe, où le groupe fait référence à des éléments de la population tels que des éléments, des personnes, etc. et la caractéristique est l'élément d'intérêt. Comme la population est très nombreuse et inconnue, la moyenne de la population est une constante inconnue. Avec la formule suivante, la moyenne de la population peut être calculée,

∑ = ajouter
a i = toutes les observations
Principales différences entre la moyenne de l'échantillon et la moyenne de la population
Les différences significatives entre la moyenne de l'échantillon et la moyenne de la population sont expliquées en détail dans les points suivants:
- La moyenne arithmétique des valeurs d'échantillonnage aléatoires tirées de la population s'appelle la moyenne de l'échantillon. La moyenne arithmétique de la population entière est appelée moyenne de population.
- L'échantillon est représenté par x̄ (prononcé comme une barre x). D'autre part, la moyenne de la population est appelée μ (terme grec mu).
- Bien que le calcul de la moyenne de l’échantillon soit facile, la liste des éléments fournis n’est que très peu, ce qui prend très peu de temps. Contrairement à la moyenne de la population, où le calcul est difficile, car de nombreux éléments de la population prennent beaucoup de temps.
- La précision d'une moyenne de population est comparativement supérieure à la moyenne de l'échantillon. La précision d'une moyenne d'échantillon peut être améliorée en augmentant le nombre d'observations.
- Les éléments de la population sont représentés par «N» dans la moyenne de la population. Au contraire, «n» dans la moyenne de l'échantillon représente la taille de l'échantillon.
- Lorsque l'écart type est calculé à l'aide de la moyenne de l'échantillon, il est désigné par la lettre 's'. Inversement, lorsque la moyenne de population est utilisée dans le calcul de l'écart type, elle est représentée par sigma (σ).
Conclusion
La méthode de calcul des deux moyennes est identique, c'est-à-dire que la somme de toutes les observations est divisée par le nombre d'observations, mais il existe une grande différence entre leur représentation. Alors que la moyenne de l'échantillon est écrite sous la forme x̄ ou parfois M, la moyenne de la population est appelée μ. La moyenne de l'échantillon est une variable aléatoire, tandis que la moyenne de la population est une constante inconnue.