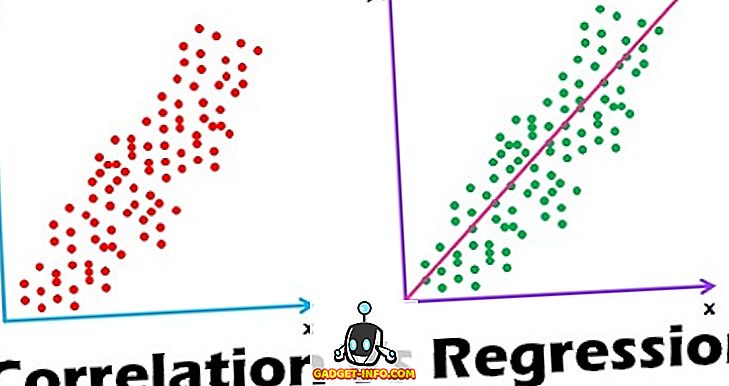
La différence entre corrélation et régression est l’une des questions les plus fréquemment posées dans les entretiens. En outre, beaucoup de gens souffrent d'ambiguïté dans la compréhension de ces deux. Alors, prenez une lecture complète de cet article pour avoir une compréhension claire sur ces deux.
Tableau de comparaison
| Base de comparaison | Corrélation | Régression |
|---|---|---|
| Sens | La corrélation est une mesure statistique qui détermine la corrélation ou l'association de deux variables. | La régression décrit comment une variable indépendante est numériquement liée à la variable dépendante. |
| Usage | Représenter une relation linéaire entre deux variables. | Ajuster une meilleure ligne et estimer une variable sur la base d’une autre variable. |
| Variables dépendantes et indépendantes | Aucune différence | Les deux variables sont différentes. |
| Indique | Le coefficient de corrélation indique dans quelle mesure deux variables se déplacent ensemble. | La régression indique l'impact d'un changement d'unité de la variable connue (x) sur la variable estimée (y). |
| Objectif | Trouver une valeur numérique exprimant la relation entre les variables. | Estimer les valeurs d'une variable aléatoire à partir des valeurs d'une variable fixe. |
Définition de corrélation
Le terme corrélation est une combinaison de deux mots "Co" (ensemble) et de relation (connexion) entre deux quantités. La corrélation est lorsque, au moment de l'étude de deux variables, il est observé qu'un changement d'unité dans une variable est répliqué par un changement équivalent dans une autre variable, c'est-à-dire directe ou indirecte. Ou alors, les variables sont dites non corrélées lorsque le mouvement d'une variable ne correspond à aucun mouvement d'une autre variable dans une direction donnée. C'est une technique statistique qui représente la force de la connexion entre des paires de variables.
La corrélation peut être positive ou négative. Lorsque les deux variables se déplacent dans le même sens, c'est-à-dire qu'une augmentation d'une variable entraîne l'augmentation correspondante d'une autre variable et inversement, les variables sont alors considérées comme corrélées positivement. Par exemple : profit et investissement.
Au contraire, lorsque les deux variables se déplacent dans des directions différentes, de sorte qu'une augmentation d'une variable entraîne la diminution d'une autre variable et inversement, cette situation est appelée corrélation négative. Par exemple : Prix et demande d'un produit.
Les mesures de corrélation sont données sous:
- Coefficient de corrélation produit-moment de Karl Pearson
- Coefficient de corrélation de rang de Spearman
- Diagramme de dispersion
- Coefficient de déviations concurrentes
Définition de régression
Une technique statistique pour estimer la variation de la variable dépendante de la métrique due à la modification d'une ou plusieurs variables indépendantes, basée sur la relation mathématique moyenne entre deux variables ou plus, est appelée régression. Il joue un rôle important dans de nombreuses activités humaines, en tant qu’outil puissant et flexible permettant de prévoir les événements passés, présents ou futurs en fonction d’événements passés ou présents. Par exemple : sur la base des enregistrements passés, le bénéfice futur d'une entreprise peut être estimé.
Dans une régression linéaire simple, il existe deux variables x et y, où y dépend de x ou dit influencé par x. Ici, y est appelée variable dépendante ou critère et x est indépendante ou variable prédictive. La droite de régression de y sur x est exprimée par:
y = a + bx
où, a = constant,
b = coefficient de régression,
Dans cette équation, a et b sont les deux paramètres de régression.
Différences clés entre corrélation et régression
Les points ci-dessous expliquent la différence entre corrélation et régression en détail:
- Une mesure statistique qui détermine la corrélation ou l'association de deux quantités est appelée corrélation. La régression décrit comment une variable indépendante est numériquement liée à la variable dépendante.
- La corrélation est utilisée pour représenter la relation linéaire entre deux variables. Au contraire, la régression est utilisée pour ajuster la meilleure ligne et estimer une variable sur la base d'une autre variable.
- En corrélation, il n'y a pas de différence entre les variables dépendantes et indépendantes, c'est-à-dire que la corrélation entre x et y est similaire à y et x. Inversement, la régression de y sur x est différente de x sur y.
- La corrélation indique la force de l'association entre les variables. Par opposition à, la régression reflète l’impact du changement d’unité de la variable indépendante sur la variable dépendante.
- La corrélation vise à trouver une valeur numérique qui exprime la relation entre les variables. Contrairement à la régression dont l’objectif est de prédire les valeurs de la variable aléatoire à partir des valeurs de la variable fixe.
Conclusion
Avec la discussion ci-dessus, il est évident qu'il existe une grande différence entre ces deux concepts mathématiques, bien que ces deux concepts soient étudiés ensemble. La corrélation est utilisée lorsque le chercheur veut savoir si les variables à l'étude sont corrélées ou non, si oui, quelle est la force de leur association. Le coefficient de corrélation de Pearson est considéré comme la meilleure mesure de corrélation. Dans l'analyse de régression, une relation fonctionnelle entre deux variables est établie afin de faire des projections futures sur les événements.